Salar Niknafs, Rian Dippenaar, Dominic Phelan

School of Mechanical, Materials and Mechatronics Engineering,
Faculty of Engineering and Information Sciences,
University of Wollongong, Australia

Dendritic structures are one of the most frequent patterns in nature, that appear in crystalline systems (such as metals), advanced ceramics and neural systems of the living organisms. A classic example is the six-fold radial symmetry of snowflakes, demonstrated in Video 1.

Every second, about 10 million metallic dendrites are produced globally during solidification processes, while the human brain alone has a hundred billion neurons, each being connected to the neighboring cells with dendritic receivers and axon terminals (transmitters) [1]. These self-organized patterns exhibit unique properties that have attracted a great deal of scholarly interest in science, engineering and design.

Embedded in the core of many industrially important processes such as casting, there is a strong relationship between the material properties and the solidified dendritic microstructures. Single crystals that are used in turbine blades (performing at extreme conditions of motion and temperature) are utilized though controlled solidification conditions that enables precisely engineered arrangement of dendrites.

From the design perspective, dendritic formations are a perfect example of “nature’s form-finding strategies” [2] which are (to a great degree) understood in terms of the underlying processes that control their response. Finally, in the simulation domain and as an interactive art form, dendrites possess the capability to organize and evolve in respond to the physical and thermal parameters. Thus the extension of these parameters into conditions well beyond the experimentally accessible regimes is an exploratory form of interaction often accompanied with unanticipated responses.

Video 1. Created by filmmaker Vyacheslav Ivanov this microscopic short shows the intimate details of fragile snowflakes as they form in their miraculous hexagonal forms. Music by Aphex Twin.

Modeling the solidification of metallic system requires a computation that takes into account the underlying physics, thermodynamics and crystallography of the system. Warren & Boettinger [3] presented a model that numerically predicts the state of systems undergoing solidification and represented it into a mesh of cells. In their model, the evolution of each individual cell is decided by the diffusion of solute elements within the grid and the fraction of each phase (field of each phase) described by the thermodynamics of the system. The latter is achieved by assigning a so called “phase-field’ equation to individual cells. The phase-field equations (and hence the name of model ‘phase-field’) are coupled with solute diffusion equations and are solved at specified time frames by minimizing the total free energy of the system.

In our proposed study [4] microstructural simulations were performed using MICRESS® code, which implements a multi-phase-field approach and essentially provides a mathematical solution to the coupled partial differential equations of phase-field and diffusion [5]. In the context of the study, MICRESS® was used to simulate the morphological transitions and the solute segregations during directional solidification under a wide spectrum of temperature gradients, solidification rates and chemical compositions. The proposed model is integrated with an in-situ experimental study of solidification in a high-temperature laser-scanning confocal microscope.

Such in-situ studies are able to provide an experimental mean to measure some of the crucial physical properties of the studied alloys, resulting in more refined microstructural simulations of such phenomena. For instance we demonstrated a real-time method for the calculation of Gibbs-Thomson coefficient and the solid-liquid interfacial energy of the studied alloys by analysing the shape of the grain-boundary grooves at the solid-liquid interface. The interface mobility parameter was calibrated so to achieve a realistic interface velocity aligned with the regime experimentally observed in real-time in the confocal microscopy.

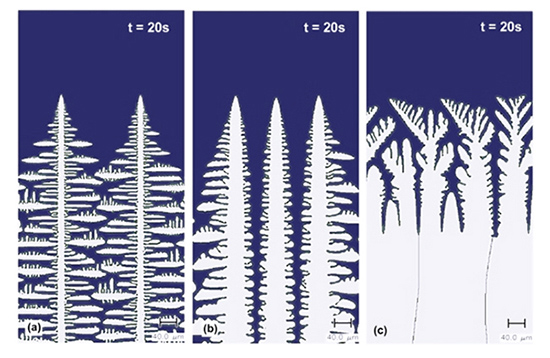
Figure 1. Changes of growth morphology from dendritic (a & b) to seaweed microstructures (c) due to an increased temperature gradient, while the cooling rate was constant.

Video 2. Solidification simulation of a high-speed casting process that is closely integrated with a high-temperature LSCM system, rendering a more realistic physical input data into the model. The computation for this model was performed in a grid that was constructed by 1000 cells in the width and 1000 cells in the initial height with a grid size of 0.1µm.

References

1. Rappaz, M., Kurz, W.: “Dendrites solidified by computer”. Nature, 375 (1995), p. 107


2. Oxman, N.: “Material-based design computation”. Thesis (Ph. D.) Massachusetts Institute of Technology, Dept. of Architecture, (2010)


3. Warren, J. A. & Boettinger, W. J.: “Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method”. Acta metal. Mater. 43 (1995), p. 689


4. Niknafs, S., Dippenaar, R.: “Experimentally-aided simulation of microstructure development during steel solidification”. ISIJ International special issue of Cutting Edge of Computer Simulation of Solidification, Casting & Refining, 54 (2014), p. 526


5. Steinbach, I., Pezzolla, F., Nestler B. and et al.: “A phase field concept for multiphase systems” Physica D, 94 (1996), p. 135